［結論］

「当量の電気の通過の熱的効果は、回路を形成する金属の長さ、太さ、形状、または種類のいかんに

かかわらず、電気の通過に対する抵抗に比例する。また、他の条件が同じならば、この効果は通過する

電流の２乗に比例する。」

ここに見いだされた関係は、今日「ジュールの法則」と呼ばれるものにほかならない。

Ｑ＝ｋ・Ｉ^２・Ｒ・ｔ

Ｑ：熱量［ｃａｌ］　　Ｉ：電流［Ａ］　　Ｒ：抵抗［Ω］　

　　　ｔ：時間［ｓ］　　　　ｋ：比例定数

上記の実験の詳細は、翌１８４１年のＰｈｉｌｏｓｏｐｈｉｃａｌ　Ｍａｇａｚｉｎｅに発表された。

その中では、以上のほかに、電池内で進行する電気分解と全回路についての

発熱量との関係にまで研究が拡張されているが、

ジュールはこの場合にも同じ法則が成立することを実験によって明らかにした。

◇課題実験２

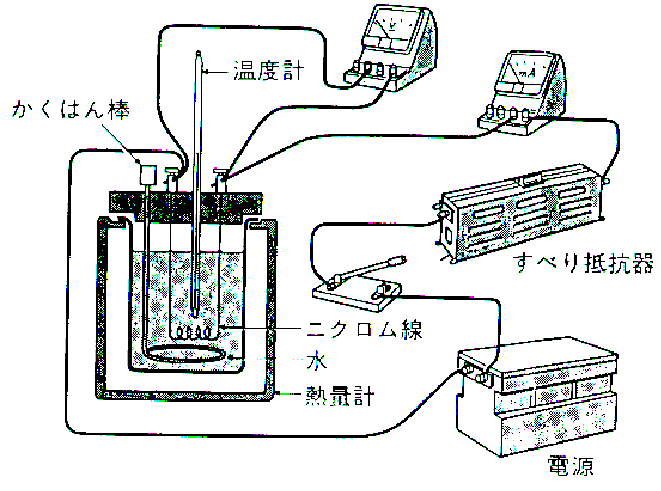
［目的］ジュールの法則を検証する。

［方法］１．図のように電源、すべり抵抗器、電流計、ニクロム線を直列につなぎ、

ニクロム線の両端に電圧計をつなぐ。

２．すべり抵抗器を調節して、ニクロム線（抵抗５．０Ω）に

一定の電流（１．０Ａ）の電流が流れるようにする。

３．５分間電流を流し、水の温度変化を測定し、発生した熱量を計算する。

４．ニクロム線の抵抗を１０Ω、１５Ω、２０Ωと変えて

同様の操作を繰り返す。

５．次に、ニクロム線の抵抗を一定（５Ω）にして、すべり抵抗器を調節して、

流れる電流を１．０Ａ、２．０Ａ、３．０Ａ、４．０Ａと変化させ、５分間電流を流し、

水の温度変化を測定し、発生した熱量を計算する。

電流(A)	電圧(V)	抵抗(Ω)	温度の変化（℃）	温度上昇	発熱量
				℃	cal

次にジュールは、電池の代わりに発電機を用いて回路に電流を流し、この電流（誘導電流）もジュールの法則に従うかどうか調べることにした。

実験２

発電機を媒介にして仕事を電流に変え、ジュール熱を測定した。

［結論］

　誘導電流の場合も、ジュールの法則に従う。

◇課題実験３

　課題実験２で、電源として発電機を用いて、同様な実験を工夫せよ。

電流(A)	電圧(V)	抵抗(Ω)	温度の変化（℃）	温度上昇	発熱量
				℃	cal

　
以上によって発電機による電流と熱の関係が判明したので、彼の次の問題は発電に要する力学的仕事と熱の関係であった。

彼は装置に工夫をこらして力学的仕事を測れるようにした。次にその装置を示すことにする。

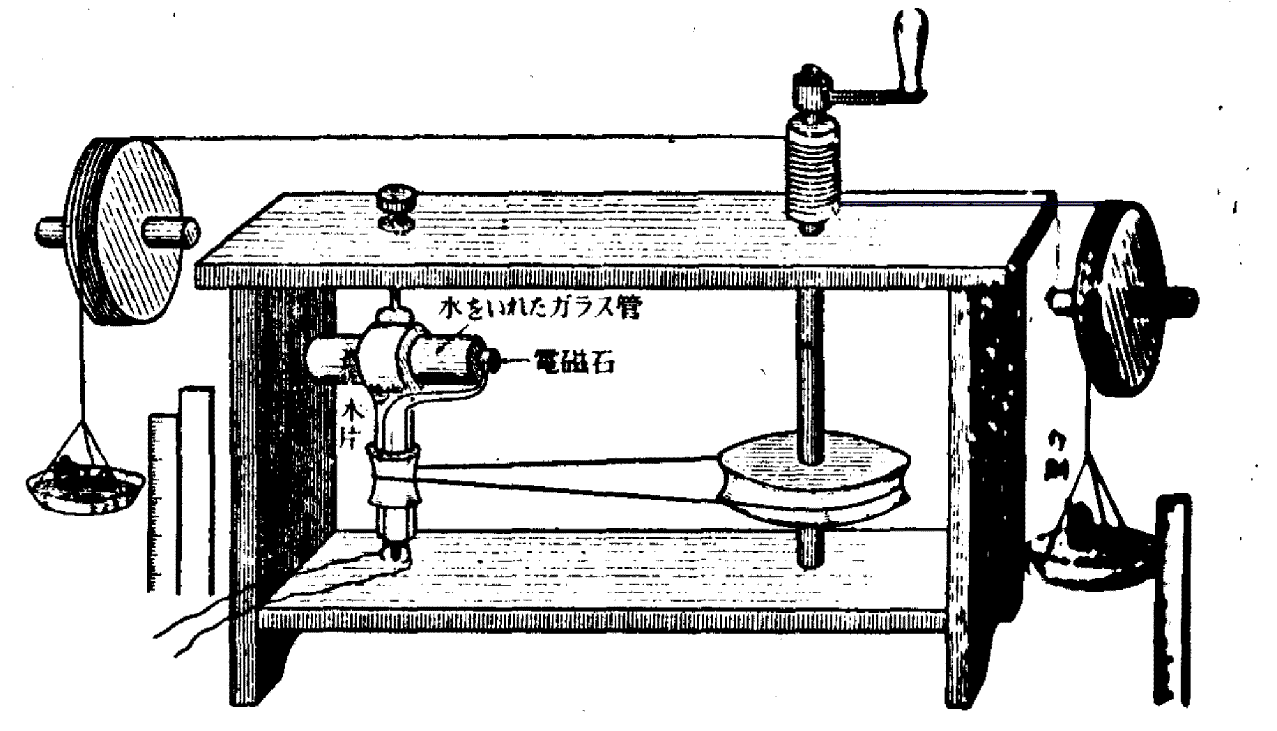
磁界 → → → →	実験３	水を入れたガラス管に電磁石をいれ、これを磁界中で回転させる。
	左図のように、回転させるべき軸に糸を巻き付け、糸は滑車を通って分銅をのせた皿につなぐ。こうすれば軸にはたらいた仕事は、分銅の重さとその降下距離とから簡単にわかる。この実験はきわめてむずかしいものであるが、彼はこれから１ポンドの水を１Ｆ暖める熱は８３８フィート・ポンドの仕事に相当するという結果を得た。

Ｑ９．上記のジュールの実験結果から、水１ｇを１℃高めるのに必要な熱量は何［Ｊ］の仕事に相当するか計算せよ。

ただし、１ポンド＝４５３ｇ、１Ｆ＝５／９℃、１フート・ポンド＝１．３６Ｊとする。